IMED2: TP2

Reconstruction tomographique (1/3)

Vous avez déjà apprivoisé la radiographie numérique rayons X, nous voici maintenant partis pour explorer l’univers de la tomographie ! La tomographie (du grec $\tau\omicron\mu\omicron\varsigma$, coupe) recouvre l’ensemble des technologies permettant de visualiser l’intérieur d’un patient (comme une tranche de jambon), sans l’ouvrir pour autant (car le jambon, dans notre cas, c’est le patient !).

Ce premier cours sur la tomographie focalise sur les mathématiques de la reconstruction tomographique. Il est plus aride que votre cours sur la radiographie numérique, mais la maîtrise des outils mathématiques appliqués à la tomographie est absolument indispensable : ce notebook doit vous aider à vous les approprier ! Vous allez également découvrir ASTRA Toolbox, dont vous trouverez les détails ici : https://www.astra-toolbox.com/

from google.colab import drive
drive.mount('/content/gdrive',force_remount=True)

import sys
from pathlib import Path
root = Path("/content/gdrive/My Drive/EPITA-2021/TP2 - Q4 2021")
sys.path.append(str(root))

import numpy as np
from pathlib import Path
import matplotlib as mpl
mpl.rc('image', cmap='gray', interpolation='none')
from matplotlib import pyplot as plt
from PIL import Image

np.random.seed(26)

root = Path.cwd()

from ipywidgets import interact

!pip install scikit-image==0.18
from skimage.draw import disk

Mounted at /content/gdrive
Requirement already satisfied: scikit-image==0.18 in /usr/local/lib/python3.7/dist-packages (0.18.0)
Requirement already satisfied: scipy>=1.0.1 in /usr/local/lib/python3.7/dist-packages (from scikit-image==0.18) (1.4.1)
Requirement already satisfied: networkx>=2.0 in /usr/local/lib/python3.7/dist-packages (from scikit-image==0.18) (2.6.3)
Requirement already satisfied: numpy>=1.16.5 in /usr/local/lib/python3.7/dist-packages (from scikit-image==0.18) (1.19.5)
Requirement already satisfied: matplotlib!=3.0.0,>=2.0.0 in /usr/local/lib/python3.7/dist-packages (from scikit-image==0.18) (3.2.2)
Requirement already satisfied: PyWavelets>=1.1.1 in /usr/local/lib/python3.7/dist-packages (from scikit-image==0.18) (1.2.0)
Requirement already satisfied: imageio>=2.3.0 in /usr/local/lib/python3.7/dist-packages (from scikit-image==0.18) (2.4.1)
Requirement already satisfied: pillow!=7.1.0,!=7.1.1,>=4.3.0 in /usr/local/lib/python3.7/dist-packages (from scikit-image==0.18) (7.1.2)
Requirement already satisfied: tifffile>=2019.7.26 in /usr/local/lib/python3.7/dist-packages (from scikit-image==0.18) (2021.11.2)
Requirement already satisfied: python-dateutil>=2.1 in /usr/local/lib/python3.7/dist-packages (from matplotlib!=3.0.0,>=2.0.0->scikit-image==0.18) (2.8.2)
Requirement already satisfied: pyparsing!=2.0.4,!=2.1.2,!=2.1.6,>=2.0.1 in /usr/local/lib/python3.7/dist-packages (from matplotlib!=3.0.0,>=2.0.0->scikit-image==0.18) (2.4.7)
Requirement already satisfied: kiwisolver>=1.0.1 in /usr/local/lib/python3.7/dist-packages (from matplotlib!=3.0.0,>=2.0.0->scikit-image==0.18) (1.3.2)
Requirement already satisfied: cycler>=0.10 in /usr/local/lib/python3.7/dist-packages (from matplotlib!=3.0.0,>=2.0.0->scikit-image==0.18) (0.11.0)
Requirement already satisfied: six>=1.5 in /usr/local/lib/python3.7/dist-packages (from python-dateutil>=2.1->matplotlib!=3.0.0,>=2.0.0->scikit-image==0.18) (1.15.0)

# !apt-get install automake libtool
# !pip install astra-toolbox

# !apt-get install automake libtool
# !git clone https://github.com/astra-toolbox/astra-toolbox
# %cd astra-toolbox/build/linux
# !./autogen.sh
# !./configure --with-cuda=/usr/local/cuda \
#              --with-python \
#              --with-install-type=module
# !make -j2
# !make install

import astra

Partie 1 - Géométrie parallèle, projection parallèle, sinogrammes

Comme présenté au début du cours, on considère la géométrie parallèles suivante :

Le principe de la reconstruction tomographique est le suivant. Dans le cas idéal, la mesure au détecteur correspond à une loi de Beer-Lambert $I=I_0e^{-p}$, d’où je peux récupérer $p$, qui est ma ligne intégrale. Si mon image est bi-dimensionnelle, $p$ est un signal mono-dimensionnel. On appelle acquisition tomographique, la collection de telles lignes intégrales $p$, lorsque l’angle des lignes intégrales couvre un certain intervalle angulaire : \(A_\Theta = \left\lbrace p_\theta \right\rbrace_{\theta\in\Theta}, \quad p_\theta(u) = \iint_{u_\theta(\underline{x})=u} \mu(\underline{x})\mathrm{d}\underline{x}.\) En géométrie parallèle, dans notre cas d’étude, $\Theta = [0,\pi]$. En mots simples, l’acquisition tomographique revient donc à collecter les projections d’un objet sous tous les angles d’un demi-cercle. En mots compliqués, l’acquisition tomographique est la transformée de Radon de $\mu$.

Le problème de la reconstruction tomographique consiste à répondre à la question suivante : Etant donnée $A_\Theta$, est-il possible de reconstruire une carte 2D des $\mu$ ? Selon que l’on se place dans un cas idéal ou non, que l’on couvre bien tout le demi-cercle $[0,\pi]$ ou non, que les projections soient tronquées ou non, etc., la réponse à cette question sera plus ou moins simple. Dans la suite, on appellera $f$, la quantité reconstruite à partir de $A_\Theta$.

Nous allons reprendre les résultats mathématiques fondamentaux qui permettent de répondre au problème de la reconstruction tomographique dans un cas idéal en géométrie parallèle 2D. Comme nous l’avons fait en radiographie numérique, nous verrons qu’il est nécessaire de réfléchir hors du cadre idéal dans les cours 2 et 3 de tomographie.

Questions

1. Quelle est l’équation qui relie le point $\underline{x}=(x,y)$ à sa coordonnée projetée $u_\theta(\underline{x})$ ?
2. On se donne un nombre nbins de bins de détecteurs (voyez cela comme un nombre de pixels sur une image à une ligne). Définissez l’axe detector, dont l’origine est au milieu du détecteur ; on s’attend à quelque chose comme : [-191.5 -190.5 -189.5 -188.5 … 188.5 189.5 190.5 191.5] lorsque nbins=384.
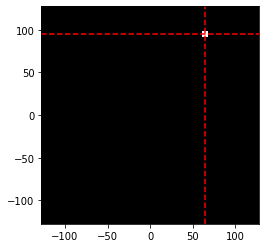
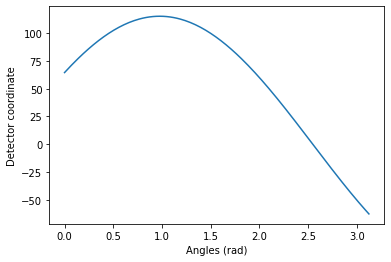
3. On définit une taille d’image N et une image synthétique, constituée d’un simple petit carré blanc sur fond noir. Afin de coller à la définition de la géométrie ci-dessus, définissez les axes X et Y afin de placer l’origine au centre de l’image, comme sur la figure ci-dessus. Déduisez-en les valeurs des coordonnées $(x_0, y_0)$ du centre du carré blanc, dans ce système de coordonnées. Vérifiez sur l’image que les lignes rouges intersectent bien le centre du carré. Attention aux axes : rappelez-vous qu’en Python, la première coordonnée donne la position verticale, la second coordonnée donne la position horizontale.
4. On définit un vecteur d’angles de $[0,\pi]$. Quelle est la trajectoire du point $(x_0,y_0)$ en fonction des angles ?
5. On utilise les fonctionnalités d’ASTRA pour créer une géométrie d’image et un projecteur (regardez la documentation d’ASTRA pour en savoir plus). Puis, on génère un sinogramme : il s’agit d’une image dont chaque ligne correspond à la projection au détecteur pour une angulation donnée (on parcourt le vecteur des angles d’acquisition en parcourant les lignes du sinogramme). Rajoutez à cette image votre estimation de la trajectoire du point $(x_0,y_0)$ : qu’observez-vous ?
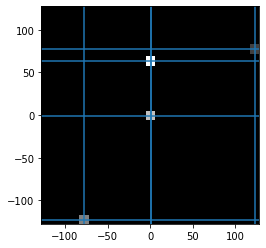
6. Faites de même pour une image avec plusieurs carrés de différents niveaux de gris ; observez le sinogramme généré : que pouvez-vous en dire ?

# Question 2
def getDetectorAxis(nbins):
    return (np.arange(nbins) - 0.5 * (nbins - 1))
nbins = 384
detector = getDetectorAxis(nbins)

N = 256
img = np.zeros((N,N))
m = 3
ctr = [32,192]
img[ctr[0]-m:ctr[0]+m+1,ctr[1]-m:ctr[1]+m+1] = 1

# Question 3
X = getDetectorAxis(img.shape[1])
Y = -getDetectorAxis(img.shape[0])
x0, y0 = X[ctr[1]], Y[ctr[0]]

plt.figure()
plt.imshow(img,extent=[X.min(),X.max(),Y.min(),Y.max()])
plt.axvline(x0,0,1,c='r',ls='--')
plt.axhline(y0,0,1,c='r',ls='--')
plt.show()

# Question 4
def getTrajectory(x0,y0,angles):
    return x0 * np.cos(angles) + y0 * np.sin(angles)

angles = np.linspace(0,np.pi,180,False)
traj = getTrajectory(x0,y0,angles)

plt.figure()
plt.plot(angles,traj)
plt.xlabel('Angles (rad)')
plt.ylabel('Detector coordinate')
plt.show()

# ASTRA framework :
# - create image geometry (NxN image array)
# - create projection geometry (parallel-beam, detector bin size, detector size, angular positions)
# - create a projector (projection method, from an image geometry to a projection geometry)
# - apply the projector to an existing image (img is adapted to the image geometry that was defined)
#   returns: an ID and a sinogram
vol_geom = astra.create_vol_geom(N,N)
proj_geom = astra.create_proj_geom('parallel', 1.0, nbins, angles)
proj_id = astra.create_projector('strip', proj_geom, vol_geom)
sinogram_id, sinogram = astra.create_sino(img, proj_id)

plt.imshow(sinogram,extent=[detector.min(),detector.max(),angles.max()*180/np.pi,angles.min()*180/np.pi])
plt.title('Sinogram')
plt.axis('auto')
plt.xlabel('Detector coordinate')
plt.ylabel('Angle (deg)')

# Question 5
plt.plot(traj,angles * 180 / np.pi,'r',alpha=0.5)

plt.show()

img = np.zeros((256,256))
m = 5
centers = [[50,250],[250,50],[128,128],[64,128]]
for i,ctr in enumerate(centers):
    img[ctr[0]-m:ctr[0]+m+1,ctr[1]-m:ctr[1]+m+1] = i+1
    # Question 6
    x0, y0 = X[ctr[1]], Y[ctr[0]]
    plt.axvline(x0,0,1)
    plt.axhline(y0,0,1)
plt.imshow(img,extent=[X.min(),X.max(),Y.min(),Y.max()])
plt.show()

sinogram_id, sinogram = astra.create_sino(img, proj_id)
plt.imshow(sinogram,extent=[detector.min(),detector.max(),angles.max()*180/np.pi,angles.min()*180/np.pi])
plt.title('Sinogram')
plt.axis('auto')
plt.xlabel('Detector coordinate')
plt.ylabel('Angle (deg)')
plt.show()

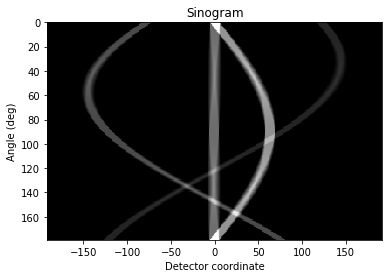
Partie 1 : Ce qu’il faut retenir

• Un peu de géométrie de lycée suffit à caractériser la géométrie d’acquisition parallèle !
• Lorsqu’on tourne autour d’un point du plan image, celui-ci se projette à différents endroits du détecteur ; sa trajectoire en fonction de l’angle d’acquisition décrit une sinusoïde.
• On représente l’acquisition $A_\Theta$ sous la forme d’un sinogramme : il s’agit simplement des profils projetés au détecteur à chaque angle d’acquisition.

Partie 2 - Rétro-projection filtrée

Rétro-projection filtrée

C’est là qu’il va falloir refaire appel à vos cours de mathématiques ! Au programme : calcul intégral, changements de variables, analyse de Fourier… et distributions de Dirac !

Tout commence avec le théorème coupe-projection qui est le suivant : \(\mathcal{F}_2[f](\rho\underline{\theta}) = \mathcal{F}_1[p_\theta](\rho),\) où : $\mathcal{F}n$ désigne la transformée de Fourier en $n$ dimensions, $f$ est l’image 2D correspondant à l’acquisition tomographique, $p\theta$ est la projection de $f$ selon l’angle $\theta$, $\rho\in\mathbb{R}$, et $\theta\in[0,\pi]$.

Questions

1. On se propose de démontrer le théorème fondamental de la reconstruction tomographique, appelé “théorème coupe-projection” :

• Partez de la définition de la transformée de Fourier 1D de $p_\theta$
• Utilisez la définition de la ligne intégrale de $p_\theta$ pour exprimer $p_\theta$ en fonction de $f$
• Trouvez une transformée de Fourier 2D dans l’expression que vous obtenez

1. Ce théorème fondamental est en réalité tout ce dont vous avez besoin pour reconstruire $f$ à partir de $A_\Theta$.
   • Ecrivez $f$ comme la transformée de Fourier inverse de $\mathcal{F}_2[f]$
   • Appliquez un changement de variables
   • Utilisez le théorème coupe-projection

Le résultat de la question 2 doit aboutir à l’inversion classique de la rétroprojection filtrée : \(f(\underline{x}) = \int_0^\pi (h * p_\theta)(u_\theta(\underline{x})) \mathrm{d}\theta,\) où $h$ est appelé le filtre rampe et correspond à une multiplication dans l’espace de Fourier par $\rho\mapsto|\rho|$. Pourquoi cette étape de filtrage est-elle vraiment nécessaire ? C’est ce qu’on va étudier dans la suite de ce notebook.

Questions

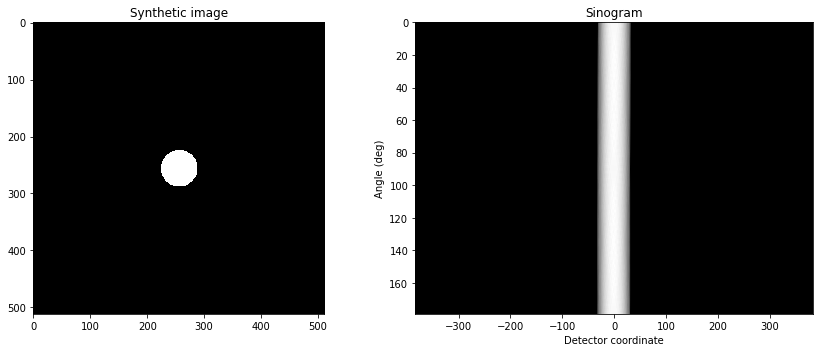
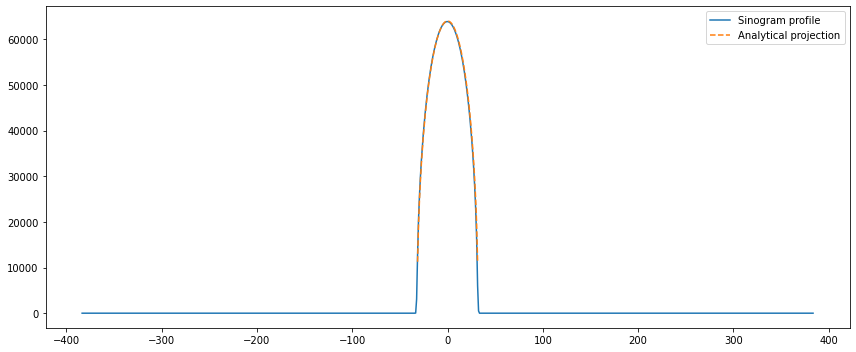
1. On génère une image synthétique constituée d’un disque uniforme centré de rayon $R$. On définit le sinogramme associé avec ASTRA (https://www.astra-toolbox.com/files/misc/ICTMS2019/20190722_ICTMS_ASTRA_workshop_2d.pdf). Auriez-vous pu calculer analytiquement la valeur de cette projection ?

On se propose de réaliser une rétroprojection “simple” (backprojection en anglais). Cela revient à reconstruire : $f_{\mathrm{BP}}(\underline{x}) = \int_0^\pi p_\theta(u_\theta(\underline{x})) \mathrm{d}\theta.$ En termes simples, la rétroprojection d’une projection $p_\theta$ revient à prendre la valeur de chaque point de $p_\theta$, et à recopier cette valeur tout le long de la ligne de projection.

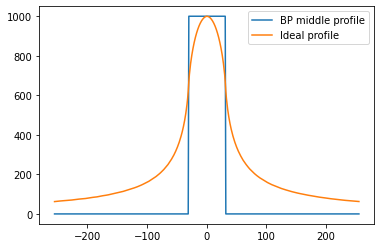
1. Observez l’image reconstruite : comment vous semble-t-elle ? Renormalisez l’image reconstruite pour que son maximum corresponde à l’image idéale. Tracez un profil horizontal au milieu de l’image pour l’image idéale et l’image reconstruite : que pouvez-vous en déduire ? L’observation sur ces profils est-elle cohérente avec votre lecture de l’image ?

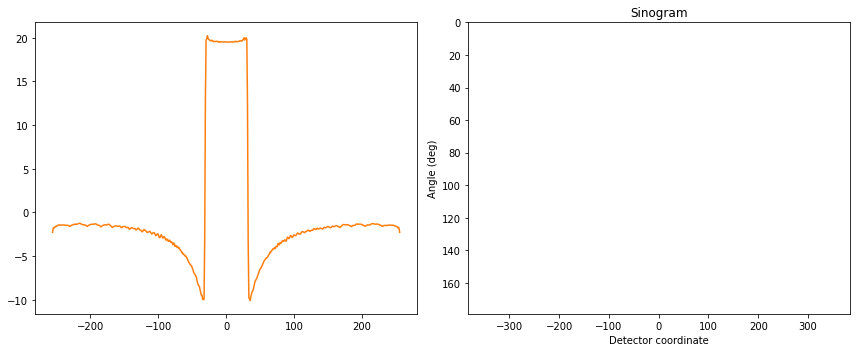
2. A vous d’ajouter le filtre rampe ! Une façon de faire est de remarquer que $

   \rho

   = \frac{1}{2\pi}(2i\pi\rho)(-i\mathrm{sign}(\rho))$. Reconnaissez-vous à quoi correspond la multiplications par $2i\pi\rho$ dans Fourier ? Et la multiplication par $-i\mathrm{sign}(\rho)$ ?

3. Réalisez un filtre rampe et appliquez-le à notre sinogramme. Tracez une ligne du sinogramme. L’effet du filtre est-il passe-bas ? passe-haut ? passe-bande ?…
4. Lancez la reconstruction du sinogramme filtré, et comparez à nouveau les profils horizontaux au centre de l’image : qu’observez-vous ?

# Question 3

angles = np.linspace(0,np.pi,180,False)
N = 512
vol_geom = astra.create_vol_geom(N,N)
nbins = int(1.5*N)
proj_geom = astra.create_proj_geom('parallel', 1.0, nbins, angles)
detector = getDetectorAxis(nbins)
proj_id = astra.create_projector('strip', proj_geom, vol_geom)

R = 32
rr, cc = disk((N//2, N//2), R, shape=(N,N))
img = np.zeros((N,N))
img[rr,cc] = 1000

sinogram_id, sinogram = astra.create_sino(img, proj_id)

f,ax = plt.subplots(1,2,figsize=(12,5))
ax[0].imshow(img)
ax[0].set_title('Synthetic image')
ax[1].imshow(sinogram,extent=[detector.min(),detector.max(),angles.max()*180/np.pi,angles.min()*180/np.pi])
ax[1].set_title('Sinogram')
ax[1].axis('auto')
ax[1].set_xlabel('Detector coordinate')
ax[1].set_ylabel('Angle (deg)')
plt.tight_layout()
plt.show()


def analyticalCenteredDiskProjection(detector,R,mu):
    """
    Projection analytique d'un disque uniforme centré de rayon R
    et de coefficient linéaire d'atténuation mu sur le détecteur detector
    """
    return 2 * mu * np.sqrt(R**2 - (detector ** 2)).clip(max = R ** 2)

plt.figure(figsize=(12,5))
plt.plot(detector,sinogram.mean(axis=0),label='Sinogram profile')
plt.plot(detector,analyticalCenteredDiskProjection(detector,R,1000),'--',label='Analytical projection')
plt.legend()
plt.tight_layout()
plt.show()

/usr/local/lib/python3.7/dist-packages/ipykernel_launcher.py:35: RuntimeWarning: invalid value encountered in sqrt

# Create a data object for the reconstruction
rec_id = astra.data2d.create('-vol', vol_geom)

# Set up the parameters for a reconstruction algorithm using the CPU
cfg = astra.astra_dict('BP')
cfg['ReconstructionDataId'] = rec_id
cfg['ProjectionDataId'] = sinogram_id
cfg['ProjectorId'] = proj_id
# cfg['FilterType'] = 'none'

# Create the algorithm object from the configuration structure
alg_id = astra.algorithm.create(cfg)

# Run the algorithm
astra.algorithm.run(alg_id)

# Get the result
rec = astra.data2d.get(rec_id) / angles.size

plt.imshow(rec)
plt.colorbar()
plt.title('BP Reconstruction')
plt.show()

# Question 4
width = (np.arange(N)-0.5*(N-1)).astype('int')
prof0 = rec[:,rec.shape[1]//2] * 1000/ np.max(rec)
prof = img[:,rec.shape[1]//2]
plt.plot(width,prof,label='BP middle profile')
plt.plot(width,prof0,label='Ideal profile')

plt.legend()
plt.show()

# Question 6

from scipy.signal import hilbert

prof = analyticalCenteredDiskProjection(detector,R,1000) *1000 / np.max(rec)
prof_grad = np.gradient(prof)
filt =  hilbert(prof_grad).imag
prof0_grad = np.gradient(prof0)
filt0 = hilbert(prof0_grad).imag

for k in range(sinogram.shape[0]):
    sinogram[k] = filt

sdiff = len(filt) - len(filt0)
f,ax = plt.subplots(1,2,figsize=(12,5))
ax[0].plot(detector,filt, label='BP profile')
ax[0].plot(detector[sdiff//2:-sdiff//2], filt0, label='Ideal profile')
ax[1].imshow(sinogram,extent=[detector.min(),detector.max(),angles.max()*180/np.pi,angles.min()*180/np.pi])
ax[1].set_title('Sinogram')
ax[1].axis('auto')
ax[1].set_xlabel('Detector coordinate')
ax[1].set_ylabel('Angle (deg)')
plt.tight_layout()
plt.show()

/usr/local/lib/python3.7/dist-packages/ipykernel_launcher.py:35: RuntimeWarning: invalid value encountered in sqrt
/usr/local/lib/python3.7/dist-packages/matplotlib/image.py:452: UserWarning: Warning: converting a masked element to nan.
  dv = np.float64(self.norm.vmax) - np.float64(self.norm.vmin)
/usr/local/lib/python3.7/dist-packages/matplotlib/image.py:459: UserWarning: Warning: converting a masked element to nan.
  a_min = np.float64(newmin)
/usr/local/lib/python3.7/dist-packages/matplotlib/image.py:464: UserWarning: Warning: converting a masked element to nan.
  a_max = np.float64(newmax)
<string>:6: UserWarning: Warning: converting a masked element to nan.
/usr/local/lib/python3.7/dist-packages/numpy/core/_asarray.py:83: UserWarning: Warning: converting a masked element to nan.
  return array(a, dtype, copy=False, order=order)

# Question 7
out_id, out = astra.creators.create_reconstruction('BP', proj_id, sinogram)
out /= angles.size*2

plt.imshow(out)
plt.show()
print(cfg)

width = np.arange(N)-0.5*(N-1)
prof = out[out.shape[0]//2]
plt.plot(width,prof,label='FBP middle profile')
plt.plot(width,img[img.shape[0]//2],label='Ideal profile')
plt.legend()
plt.grid()
plt.show()

/usr/local/lib/python3.7/dist-packages/matplotlib/image.py:452: UserWarning: Warning: converting a masked element to nan.
  dv = np.float64(self.norm.vmax) - np.float64(self.norm.vmin)
/usr/local/lib/python3.7/dist-packages/matplotlib/image.py:459: UserWarning: Warning: converting a masked element to nan.
  a_min = np.float64(newmin)
/usr/local/lib/python3.7/dist-packages/matplotlib/image.py:464: UserWarning: Warning: converting a masked element to nan.
  a_max = np.float64(newmax)
<string>:6: UserWarning: Warning: converting a masked element to nan.
/usr/local/lib/python3.7/dist-packages/numpy/core/_asarray.py:83: UserWarning: Warning: converting a masked element to nan.
  return array(a, dtype, copy=False, order=order)

{'type': 'BP', 'ReconstructionDataId': 12, 'ProjectionDataId': 10, 'ProjectorId': 8}

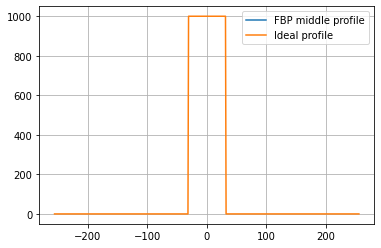
On peut directement appliquer le filtre rampe en choisissant non pas une rétroprojection simple (BP) mais une rétroprojection filtrée (FBP). C’est ce qui est fait ci-dessous. Le résultat est normalisé par la taille d’un bin détecteur.

cfg = astra.astra_dict('FBP')
cfg['ReconstructionDataId'] = rec_id
cfg['ProjectionDataId'] = sinogram_id
cfg['ProjectorId'] = proj_id
cfg['FilterType'] = 'ram-lak'

# Create the algorithm object from the configuration structure
alg_id = astra.algorithm.create(cfg)

# Run 20 iterations of the algorithm
# This will have a runtime in the order of 10 seconds.
astra.algorithm.run(alg_id)

# Get the result
rec = astra.data2d.get(rec_id)

plt.imshow(rec)
plt.colorbar()
plt.title('Reconstruction')
plt.show()

width = np.arange(N)-0.5*(N-1)
prof = rec[rec.shape[0]//2]
plt.plot(width,prof,label='FBP middle profile')
plt.plot(width,img[img.shape[0]//2],label='Ideal profile')
plt.legend()
plt.grid()
plt.show()

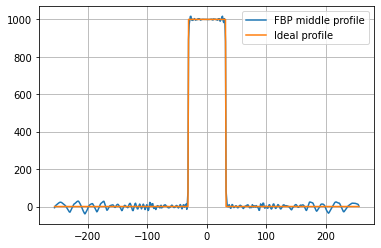
En regardant l’image avec un fenêtrage plus serré autour de zéro, on voit apparaître des motifs dans le fond de l’image : ce sont des motifs typiques de phénomènes d’interpolation liés à l’implémentation des projecteurs / rétroprojecteurs. Regardez cette image avec ou sans zoom !

zoom = slice(150,-150),slice(150,-150)
zoom = slice(None,None)
plt.imshow(rec[zoom],vmin=-20,vmax=20)
plt.colorbar()
plt.title('Reconstruction')
plt.show()

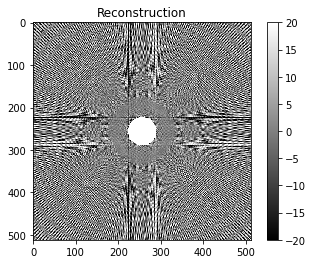
Partie 2 : Ce qu’il faut retenir

• La rétroprojection simple est un opérateur qui redistribue un profil projeté le long de sa direction de projection.
• La rétroprojection simple ne reconstruit pas l’image attendue ; pour reconstruire l’image, un pré-filtrage des projections par le filtre rampe est nécessaire.
• ASTRA Toolbox permet de réaliser ces reconstructions.

Partie 3 - Echantillonnage angulaire

Dans cette partie, nous allons commencer à toucher du doigt les problématiques d’échantillonnage angulaire. La formule FBP est une formule continue, que l’on discrétise ensuite pour en faire un algorithme : on boucle sur chaque projection, on filtre, on rétroprojette en accumulant le résultat dans un buffer. Que se passe-t-il si le nombre de projections n’échantillonne plus correctement l’intervalle $[0,\pi]$ ?

On se construit à nouveau une image synthétique, constituée d’un disque centré, et d’un point de très fort contraste.

highIntensity = True
N = 512
R = 32
img = np.zeros((N,N))
rr, cc = disk((N//2, N//2), R, shape=(N,N))
img[rr,cc] = 1000
if highIntensity:
    rr, cc = disk((N//2, N//5), R//8, shape=(N,N))
    img[rr,cc] += 5000
plt.imshow(img)
plt.colorbar()

<matplotlib.colorbar.Colorbar at 0x7fbe107756d0>

Questions

1. Définissez deux fonctions, project et reconstruct, pour automatiser la projection et la reconstruction.
   • project prend en entrée une image, un nombre d’angles, et un offset ; cela permet de créer un vecteur d’angles entre angleOffset et angleOffset+np.pi, dont la taille est donnée par le nombre d’angles. On peut ensuite créer la géométrie de projection, le détecteur, le projecteur, et le sinogramme.
   • reconstruct prend en entrée un identifiant ASTRA d’un projecteur, un identifiant ASTRA d’un sinogramme, et crée un reconstructeur FBP, qu’on utilisera pour reconstruire une image.
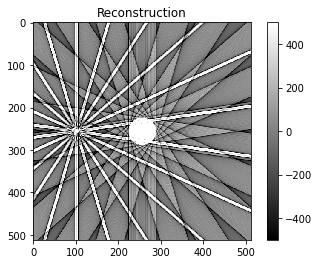
2. Lancez les différentes expériences, en générant différents sinogrammes avec un nombre décroissant de vues, et en reconstruisant les images à partir de ces sinogrammes. Qu’observez-vous ?

# Question 1

def project(img,nAngles,angleOffset=0):
    angles = np.linspace(angleOffset, angleOffset + np.pi, nAngles, False)
    N = img.shape[0]
    vol_geom = astra.create_vol_geom(N,N)
    nbins = int(1.5*N)
    proj_geom = astra.create_proj_geom('parallel', 1.0, nbins, angles)
    detector = getDetectorAxis(nbins)
    proj_id = astra.create_projector('strip', proj_geom, vol_geom)
    sinogram_id, sinogram = astra.create_sino(img, proj_id)
    return proj_id, sinogram_id, sinogram, angles, vol_geom

def reconstruct(proj_id, sinogram_id, vol_geom):
    rec_id = astra.data2d.create('-vol', vol_geom)
    cfg = astra.astra_dict('FBP')
    cfg['ReconstructionDataId'] = rec_id
    cfg['ProjectionDataId'] = sinogram_id
    cfg['ProjectorId'] = proj_id
    cfg['FilterType'] = 'ram-lak'
    alg_id = astra.algorithm.create(cfg)
    astra.algorithm.run(alg_id)
    rec = astra.data2d.get(rec_id)
    return rec

# Question 2
for nAngles in 180//2**np.arange(5):
    print(nAngles)
    # projection de img avec nAngles vues
    proj_id, sinogram_id, sinogram, angles, vol_geom = project(img, nAngles)
    # reconstruction
    rec = reconstruct(proj_id, sinogram_id, vol_geom)
    plt.imshow(rec,vmin=-500,vmax=500)
    plt.colorbar()
    plt.title('Reconstruction')
    plt.show()
    plt.plot(rec[rec.shape[0]//2])
    plt.show()

180

90

45

22

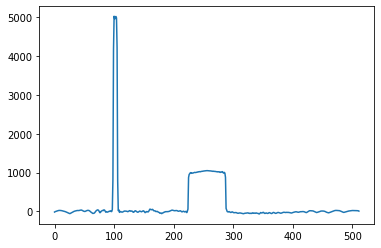
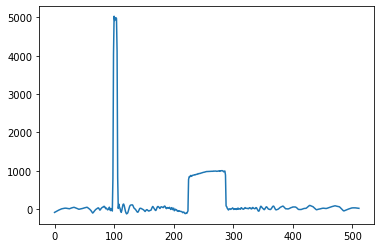
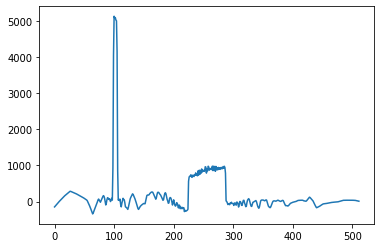
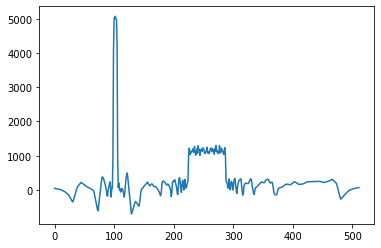
11

Dans cette dernière expérience, on génère une image très grande (de taille 5120x5120), dans laquelle on n’a qu’un petit disque (de rayon 8 !).

N = 5120
R = 8
img = np.zeros((N,N))
rr, cc = disk((N//2, N//2), R, shape=(N,N))
img[rr,cc] = 1000
zoom = slice(img.shape[0]//2-128,img.shape[0]//2+128), slice(img.shape[1]//2-128,img.shape[1]//2+128)
plt.imshow(img[zoom])
plt.colorbar()
plt.show()

Questions

1. Choisissez nAngles=32 vues, et générez un sinogramme à partir de cette image. Cela peut prendre un peu de temps, l’image est plus grande qu’avant !
2. Reconstruisez l’image à partir de ce sinogramme, et visualisez l’image avec le petit zoom proposé (afin de mieux voir les artefacts d’échantillonnage). Là encore, soyez patient !
3. Regénérez un sinogramme à partir de cette reconstruction, mais cette fois-ci, décalez les angles d’acquisition d’un demi-pas d’échantillonnage angulaire. Que remarquez-vous sur le sinogramme obtenu ?
4. Justifiez ce résultat mathématiquement ! Repartez cette fois de l’algorithme FBP en tant que boucle sur les angles d’acquisition, et remontez jusqu’au plan de Fourier !…

# Question 3
nAngles = 32
vol_geom = astra.create_vol_geom(N,N)
nbinsIdeal = int(1.5*N)
proj_id, sinogram_id, sinogram, angles, vol_geom = project(img, nAngles)

# Question 4
rec = reconstruct(proj_id, sinogram_id, vol_geom)

plt.imshow(rec,vmin=-100,vmax=100,interpolation='none')
plt.show()

zoom = slice(rec.shape[0]//2-128,rec.shape[0]//2+128),slice(rec.shape[1]//2-128,rec.shape[1]//2+128)
plt.imshow(rec[zoom],vmin=-100,vmax=100,interpolation='none')
plt.colorbar()

<matplotlib.colorbar.Colorbar at 0x7fbe0a33dfd0>

# Question 5
angleOffset = np.gradient(angles).mean() * 0.5
proj_id, sinogram_id, sinogram, angles, vol_geom = project(rec, nAngles, angleOffset)
plt.imshow(sinogram)
plt.axis('auto')
plt.colorbar()
plt.show()

# Question 5
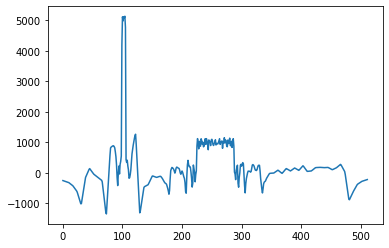
plt.plot(sinogram.mean(axis=0))
plt.axhline(0,0,1,color='r')
print(np.median(sinogram))

0.0

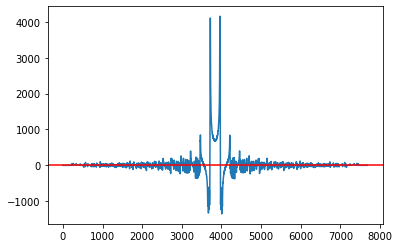
Partie 3 : Ce qu’il faut retenir

• FBP, en tant qu’algorithme, rétroprojette des projections filtrées avec leurs rebonds liés au filtre rampe.
• Lorsque l’échantillonnage angulaire diminue, ces rebonds ne se compensent plus entre eux et ils deviennent visibles dans l’image sous forme de stries de sous-échantillonnage.
• Ces stries sont intrinsèquement liées au peuplement du plan de Fourier de l’image reconstruite.