Reconstruction tomographique (2/3)

Vous avez tous les outils pour comprendre la reconstruction tomographique 2D en géométrie parallèle dans le cadre idéal : à partir des lignes intégrales (transformée de Radon), il est possible via le théorème coupe-projection de récupérer l’objet correspondant aux projections (rétroprojection filtrée). Cette théorie est bien jolie, mais… la réalité est assez différente ! Le but de ce Notebook est de vous familiariser avec un certain nombre de non-idéalités des systèmes tomographiques, et d’identifier les effets de ces non-idéalités dans les images reconstruites. Nous passerons en revue :

Une non-idéalité du tube : son caractère intrinsèquement polychromatique
Une non-idéalité du détecteur : la présence de gains et d’offsets (cela doit vous dire quelque chose !)
Une non-idéalité liée aux interactions photon/matière : le diffusé

Mais il existe de nombreuses autres sources de non-idéalités, par exemple une non-idéalité liée à l’objet lui-même (ou au patient) : la présence de mouvement au cours de l’acquisition (avez-vous des exemples en tête ?)

  
import numpy as np
from matplotlib import pyplot as plt
from skimage.draw import circle, disk
from skimage.transform import radon, iradon
import matplotlib as mpl
mpl.rc('image', cmap='gray', interpolation='none')

Partie 1 - Durcissement de faisceau

On se donne un vecteur d’angles theta. Puis, on construit deux images via la fonction buildImage. Cette fonction prend en entrée une énergie en keV, et génère une image constituée d’os, de matière molle du cerveau, et d’iode (cas d’une imagerie vasculaire avec injection de produit de contraste). Les coefficients d’atténuation dépendant de l’énergie considérée, nous pouvons avoir deux images différentes selon que l’on se place à 80 keV ou à 100 keV. Vous remarquerez que j’ai aussi ajouté un facteur de dilution de l’iode : c’est que l’on n’injecte pas toujours de l’iode pure dans le corps du patient !

Lancez les deux cellules suivantes.

  
N = 360
theta_min = 0.*np.pi
theta_max = 180.0+theta_min
theta = np.linspace(theta_min, theta_max, N, endpoint=False)

  
# in g/cm3
dilution = 0.25
densities = {'Brain':1.043,
             'Bone': 1.8,
             'Iodine': 4.93*dilution
            }
massAttenuationCoefficient = {'Brain':  {80: 1.831e-1,
                                        100: 1.701e-1},
                              'Bone':   {80: 2.229e-1,
                                        100: 1.855e-1},
                              'Iodine': {80: 3.51,
                                        100: 1.942}
                             }
def buildImage(kev):
    N = 256
    img = np.zeros((N,N))
    rr, cc = disk(((N-1)*0.5,(N-1)*0.5),(N-1)*0.45)
    img[rr,cc] = massAttenuationCoefficient['Bone'][kev]*densities['Bone']
    rr, cc = disk(((N-1)*0.5,(N-1)*0.5),(N-1)*0.4)
    img[rr,cc] = massAttenuationCoefficient['Brain'][kev]*densities['Brain']
    rr, cc = disk(((N-1)*0.25,(N-1)*0.5),10)
    img[rr,cc] = massAttenuationCoefficient['Iodine'][kev]*densities['Iodine']
    rr, cc = disk(((N-1)*0.65,(N-1)*0.7),10)
    img[rr,cc] = massAttenuationCoefficient['Iodine'][kev]*densities['Iodine']
    rr, cc = disk(((N-1)*0.65,(N-1)*0.3),10)
    img[rr,cc] = massAttenuationCoefficient['Iodine'][kev]*densities['Iodine']
    return img

img = {80:buildImage(80), 100:buildImage(100)}

fig, ax = plt.subplots(1,2,figsize=(12,4))
ax[0].imshow(img[80],vmin=0,vmax=0.5)
ax[0].set_title('80 keV')
ax[1].imshow(img[100],vmin=0,vmax=0.5)
ax[1].set_title('100 keV')
plt.show()

png

Nous allons générer les sinogrammes correspondant à ces deux images. Si ASTRA est une très bonne toolbox pour vous amuser à générer différentes géométries d’acquisition, utiliser des algorithmes de reconstruction itérative, etc., il existe également une fonction standard de scikit-image pour la géométrie parallèle 2D : radon pour la projection, et iradon pour la reconstruction. On écrira, pour projeter une image selon un vecteur d’angles theta :

radon(img, theta=theta, circle=True, preserve_range=True)

De même, pour reconstruire l’image à partir de son sinogramme, on écrira :

iradon(sino, theta=theta, circle=True)

Questions

Générez les sinogrammes des deux images ci-dessus.
Reconstruisez les images issues de ces sinogrammes.

  
# Question 1
# Sauvez les sinogrammes dans un dictionnaire :
# p = {80: **sinogramme à 80 keV** ; 100: **sinogramme à 100 keV**}
p = {80:radon(img[80], theta=theta, circle=True, preserve_range=True),
    100:radon(img[100], theta=theta, circle=True, preserve_range=True)}
fig, ax = plt.subplots(1,2,figsize=(12,4))
im0 = ax[0].imshow(p[80].T)
fig.colorbar(im0,ax=ax[0])
ax[0].axis('auto')
ax[0].set_title('80 keV')
im1 = ax[1].imshow(p[100].T)
fig.colorbar(im1,ax=ax[1])
ax[1].axis('auto')
ax[1].set_title('100 keV')
plt.show()

png

  
# Question 2
# Sauvez les reconstructions dans un dictionnaire :
# mono = {80: **reconstruction à 80 keV** ; 100: **reconstruction à 100 keV**}
mono = {80:iradon(p[80], theta=theta, circle=True),
    100:iradon(p[100], theta=theta, circle=True)}

fig, ax = plt.subplots(1,2,figsize=(12,4))
ax[0].imshow(mono[80],vmin=0,vmax=0.5)
ax[0].set_title('80 keV')
ax[1].imshow(mono[100],vmin=0,vmax=0.5)
ax[1].set_title('100 keV')
plt.show()

png

Le modèle de Beer-Lambert polychromatique empêche la possibilité de récupérer la partie linéaire, puisque : $I = \int_{\mathrm{spectre}} I_0(E)e^{-p(E)}dE.$ En supposant (c’est encore une nouvelle simplification, mais elle suffira à illustrer le problème) que le spectre est constitué uniquement de deux énergies $E_0$ et $E_1$, l’intensité reçue est donc $I=I_0(E_0)e^{-p(E_0)}+I_0(E_1)e^{-p(E_1)}$, qu’on peut réécrire de la façon suivante : $I = I_0\left(a\times e^{-p(E_0)}+(1-a)\times e^{-p(E_1)}\right)$ avec $a\in[0,1]$. Si on utilise la transformation $I\mapsto \log(I_0)-\log(I)$, comme on le fait en monochromatique, on obtient ici une projection $p_E$ égale à $p_E = \log(I_0)-\log\left(a\times e^{-p(E_0)}+(1-a)\times e^{-p(E_1)}\right).$

On se propose de simuler une acquisition polychromatique, c’est-à-dire, une acquisition issue d’un faisceau de rayons X distribué sur plusieurs énergies. Le plus simple est de considérer une approximation bichromatique du faisceau. Dans ce contexte, on considère que les photons X incidents sont de deux énergies, à savoir 80 keV et 100 keV. La probabilité que le photon incident soit à 80 keV est donnée par $P(80) = a_{80}$, et celle d’avoir un photon incident à 100 keV est $P(100)=1-P(80)$.

Questions

Avec une telle distribution de probabilité, et les sinogrammes précédemment calculés à 80 keV et 100 keV, quelle est l’intensité reçue au détecteur ?
Calculez la projection $p_E$ dans la fonction bichromatic (on suppose $I_0=1$) ; attention : les sinogrammes que vous avez calculés sont en unités “pixels” ; il faut se remettre en centimètres pour prendre des exponentielles qui aient un sens.
Reconstruisez l’image à partir de ce sinogramme : qu’observez-vous ?

  
# Question 4
def bichromatic(p,a80=0.66):
    pixel2cm = 0.1
    return -np.log(a80*np.exp(-pixel2cm*p[80]) + (1 - a80)*np.exp(-pixel2cm*p[100]))/pixel2cm

a80 = 0.66
sinogram = bichromatic(p,a80)

fig, ax = plt.subplots(1,3,figsize=(18,4))
ax[0].imshow(p[80].T)
ax[0].axis('auto')
ax[0].set_title('80 keV')
ax[1].imshow(p[100].T)
ax[1].axis('auto')
ax[1].set_title('100 keV')
ax[2].imshow(sinogram.T)
ax[2].axis('auto')
ax[2].set_title('Bichromatic')
plt.show()

png

  
# Question 5
out = iradon(sinogram, theta=theta, circle=True)
plt.imshow(out,vmin=0,vmax=0.25)
plt.colorbar()

<matplotlib.colorbar.Colorbar at 0x7fce5a3361f0>

png

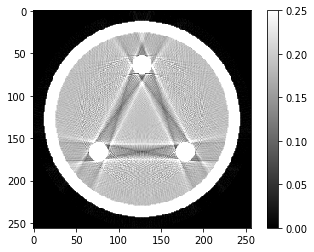
On se propose de comprendre l’origine de ces artefacts (dits de durcissement de faisceau).

Questions

Générez un vecteur d’épaisseurs en cm, variant de zéro à 45 cm (choisissez $n=500$ échantillons). Pour chaque épaisseur testée $T$, calculez $T\times \mu_{\mathrm{iodine}}(\mathrm{keV})$ pour 80 keV et 100 keV.
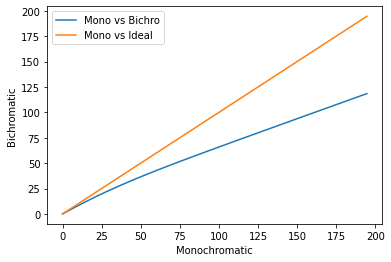
Utilisez la fonction bichromatic pour calculer la projection bichromatique de $T\mu_{\mathrm{iodine}}$, et tracez ce vecteur en fonction du vecteur correspondant à une acquisition monochromatique à 80 keV. Qu’observez-vous ? Pouvez-vous relier cette observation aux artefacts de l’image ci-dessus ?
On veut “recaler” les mesures bichromatiques à leurs mesures “idéales” monochromatiques à 80 keV. Utilisez la fonction np.polyfit à l’ordre 3 pour obtenir un fit polynomial.

  
# Question 6
# Sauvez les T*µ dans un dictionnaire comme fait avec les sinogrammes et reconstructions précédentes
x = np.linspace(0, 45, 500)
iodineProjection = {kev : x * mu * densities['Iodine'] for kev, mu in massAttenuationCoefficient['Iodine'].items()}

  
# Question 7
# y est la projection bichromatique
# x0 est la projection monochromatique
y = bichromatic(iodineProjection, a80)
x0 = iodineProjection[80]
plt.plot(x0,y, label='Mono vs Bichro')
plt.plot(x0,iodineProjection[80], label='Mono vs Ideal')
plt.xlabel('Monochromatic')
plt.ylabel('Bichromatic')
plt.legend()
plt.show()

png

  
# Question 8
params = np.polynomial.polynomial.Polynomial.fit(y, x0, 3)
polynomial = params
print(params)

88.09429686309687 + 103.43751237094426·x¹ + 9.090711918937586·x² -
6.380448144804321·x³

  
plt.plot(y,polynomial(y)-x0)

[<matplotlib.lines.Line2D at 0x7fce5a115970>]

png

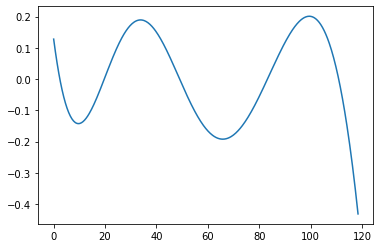
On se propose d’utiliser ce fit polynomial pour corriger l’image. Pour cela, et en première approximation, nous allons supposer que les artefacts observés viennent uniquement des inserts d’iode. Ceux-ci sont reconstruits correctement, avec peut-être une valeur à l’intérieur de l’insert légèrement différente de la vraie valeur, mais en tout cas, ces inserts sont identifiables. Ils sont aussi beaucoup plus intenses que les autres structures de l’image reconstruite.

Questions

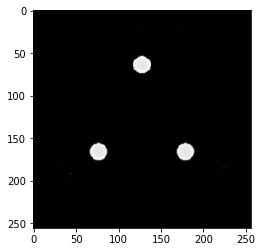
Trouvez manuellement un seuil qui vous permette d’isoler les inserts d’iode dans l’image reconstruite.
Projetez les valeurs de ces inserts d’iode ; transformez le sinogramme obtenu en utilisant le polynôme trouvé précédemment.
Reconstruisez une image à partir de ce sinogramme transformé.
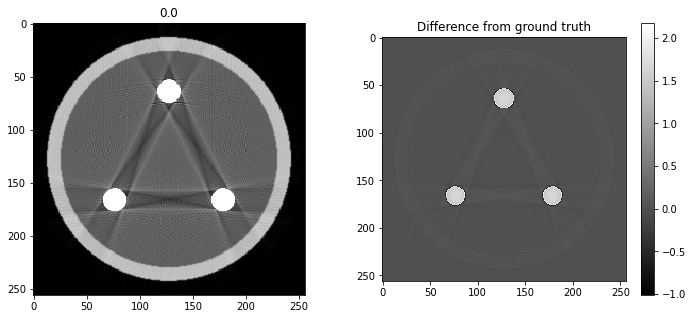
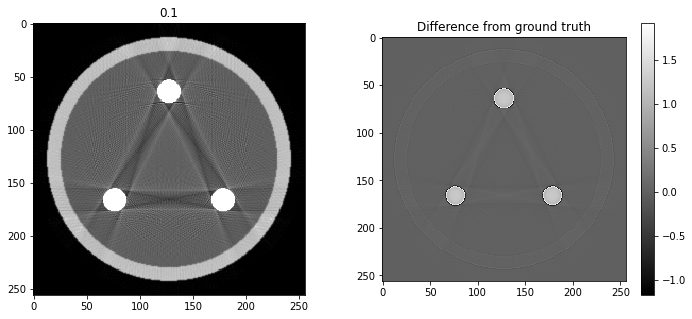
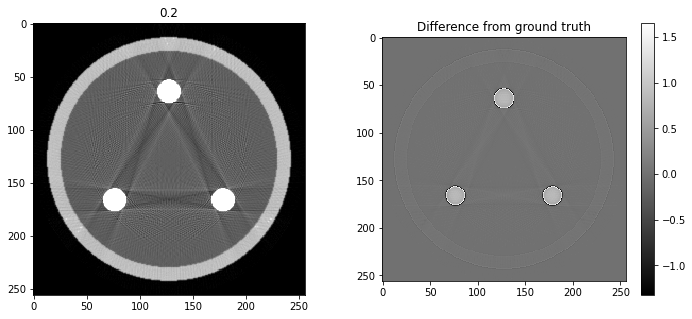
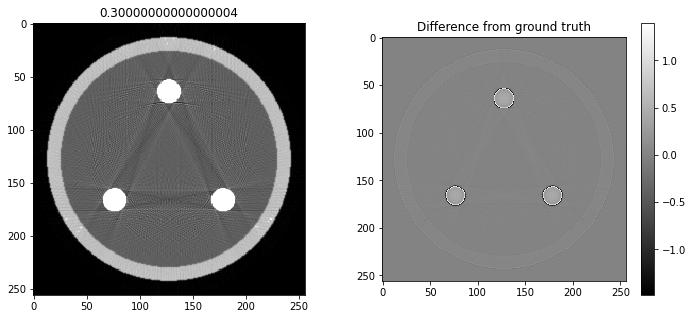
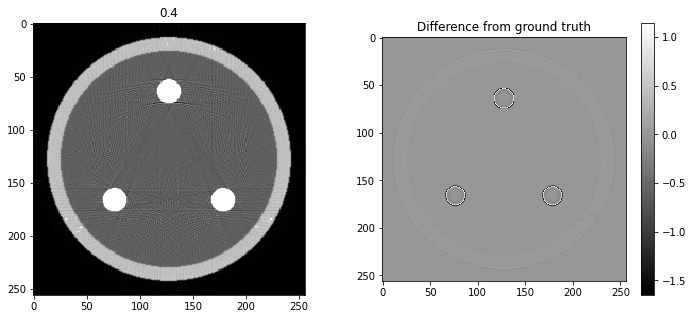
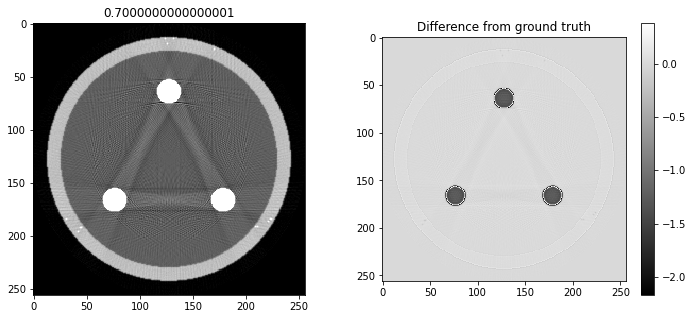
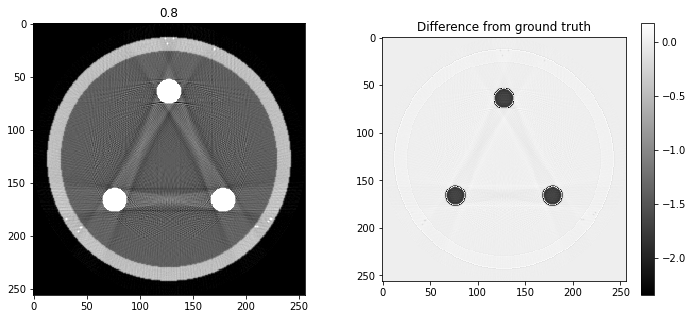
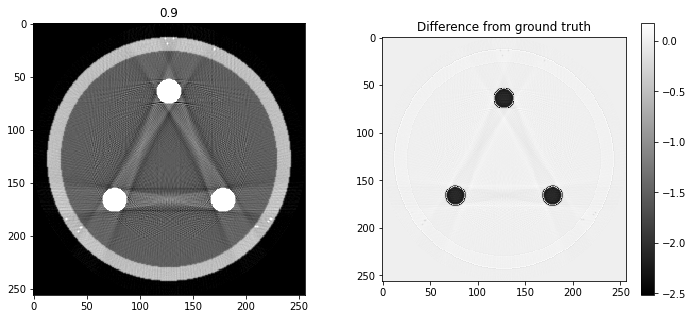
Lancez la boucle d’images suivante : qu’observez-vous ?

  
# Question 9
seg = out.copy()
seg[seg < 0.4] = 0
plt.imshow(seg)

<matplotlib.image.AxesImage at 0x7fce5a606820>

png

  
# Question 10
segProj = radon(seg, theta=theta, circle=True, preserve_range=True)
plt.imshow(segProj.T)
plt.show()

tmp = polynomial(segProj)
plt.imshow(tmp.T)

png

<matplotlib.image.AxesImage at 0x7fce5a5df2b0>

png

  
# Question 11
reproj = iradon(tmp, theta=theta, circle=True)

plt.imshow(reproj,vmin=0,vmax=0.25)
plt.colorbar()

<matplotlib.colorbar.Colorbar at 0x7fce5a02cd00>

png

  
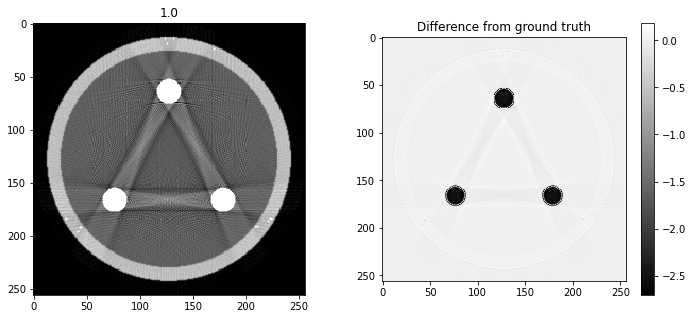
# Question 12
search = np.linspace(0,1,11)
for alpha in search:
    rec = out+alpha*reproj
    f,ax = plt.subplots(1,2,figsize=(12,5))
    ax[0].imshow(rec,vmin=0,vmax=0.5)
    ax[0].set_title(alpha)
    im = ax[1].imshow(img[80]-rec)
    f.colorbar(im,ax=ax[1])
    ax[1].set_title('Difference from ground truth')
    plt.show()

png

Partie 2 - Non-idéalités du détecteur

Un détecteur présente plusieurs non idéalités ; en premier lieu, il présente des dérives en gains et en offsets. Cela signifie que la mesure faite au niveau d’une cellule du détecteur (un pixel d’un détecteur plan, ou un bin d’un détecteur linéaire), au lieu de mesurer l’intensité $I$ des photons X qui arrivent à la cellule, on mesure $I_c = \alpha I + \beta.$ $\alpha$ est un gain (proche de 1 généralement), et $\beta$ est un offset. Si on ne fait pas attention à $\alpha$ et $\beta$, on se retrouve avec une projection corrompue $p_c = \log(I_0)-\log(I_c)$.

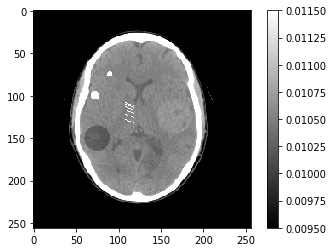
Chargez l’image ci-dessous, et regardez son sinogramme :

  
scale = 1e-5
img = np.fromfile('CTscan.raw',dtype='float32').reshape((256,256))*scale
ctDisplay = {'vmin':950*scale,'vmax':1150*scale}
plt.imshow(img,**ctDisplay)
plt.colorbar()

<matplotlib.colorbar.Colorbar at 0x7fce56e10fd0>

png

  
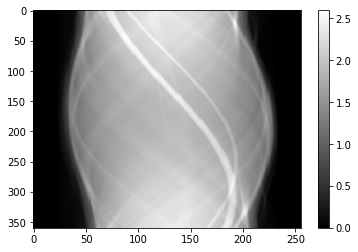
sinogram0 = radon(img, theta=theta, circle=True, preserve_range=True)

#sinogram0[100] = (sinogram0[99] + sinogram0[101]) / 2
#sinogram0[100] *= 0.9
plt.imshow(sinogram0.T, aspect='auto')
plt.colorbar()

<matplotlib.colorbar.Colorbar at 0x7fce56d6cd60>

png

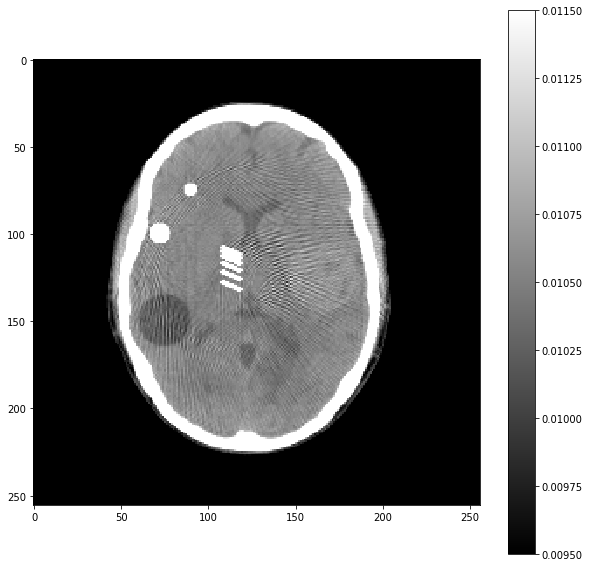
Reconstruisez l’image à partir de ce sinogramme :

  
img_ = iradon(sinogram0, theta=theta, circle=True)
plt.figure(figsize=(10,10))
plt.imshow(img_,**ctDisplay)
plt.colorbar()

<matplotlib.colorbar.Colorbar at 0x7fce56ca4b80>

png

Questions

Partant du détecteur utilisé pour le sinogramme précédent (de taille sinogram.shape[0]), générer un vecteur de gains égaux à 1 et un vecteur d’offsets égaux à 0 (cas idéal). Corrompez le vecteur de gain tous les n bins par un bruit d’écart-type de 1%. Affichez le vecteur des gains. Générez le sinogramme qui aurait été obtenu si la mesure avait subi ces gains à chaque acquisition. Reconstruisez l’image : qu’observez-vous comme artefacts ?
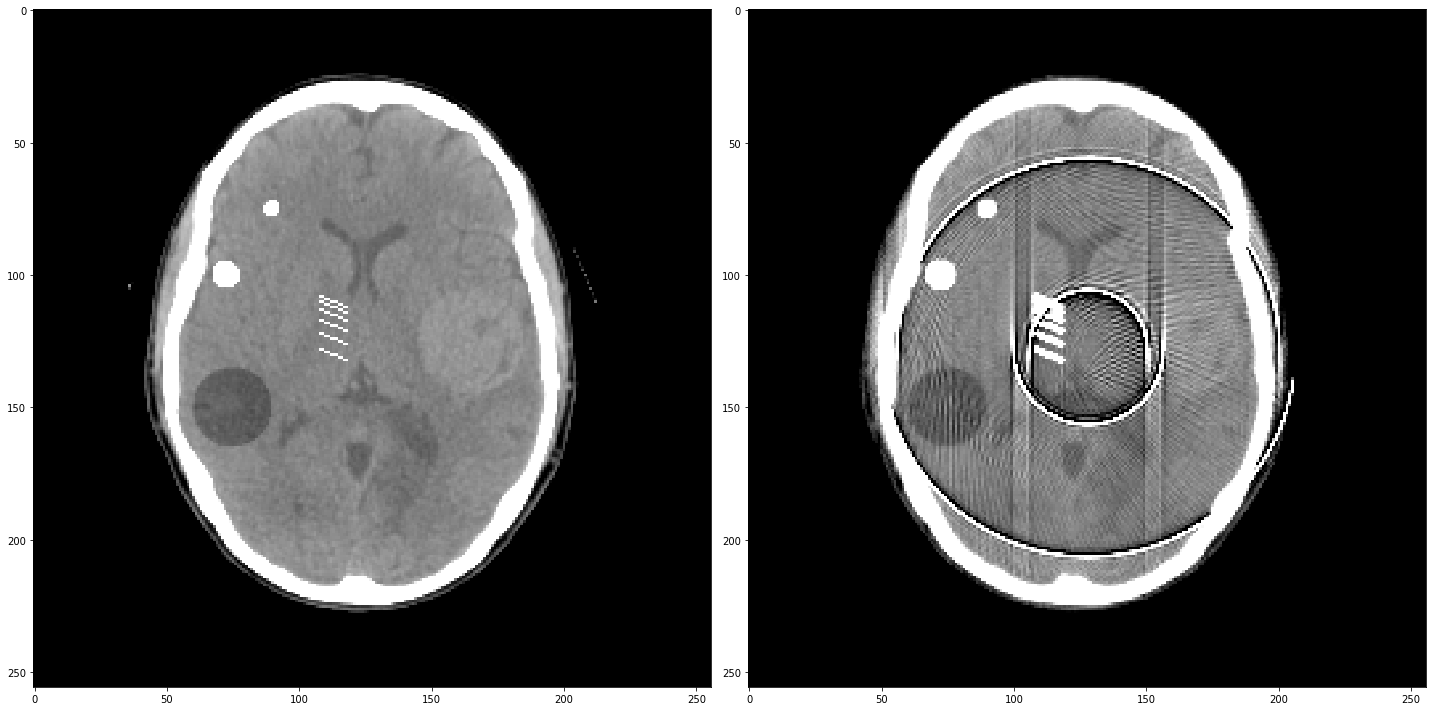
Corrompez le vecteur d’offsets tous les n bins (en partant de n//2 cette fois) par un bruit d’écart-type de 1%. Affichez le vecteur des offsets. Générez le sinogramme qui aurait été obtenu si la mesure avait subi ces gains et ces offsets à chaque acquisition. Reconstruisez l’image : qu’observez-vous comme artefacts ? (Fixez I0=10)
Changez la valeur de I0 à 100, 1000, 10000 : qu’observez-vous ? Quels artefacts disparaissent / se maintiennent ? Pourquoi ?

  
sinogram = sinogram0.copy()
np.random.seed(42)
n = sinogram.shape[0] // 5
# Question 1
# Vecteur de gains
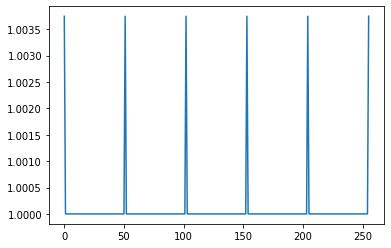
gain = np.ones(sinogram.shape[0])
gain[::n] += np.random.rand() * 0.01

plt.figure()
plt.plot(gain)
plt.show()

# Question 2
# Vecteur d'offsets
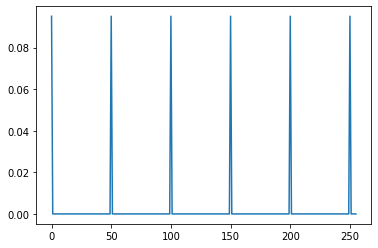
offset = np.zeros(sinogram.shape[0])
offset[::n-1] += np.random.rand() * 0.1

plt.figure()
plt.plot(offset)
plt.show()

I0 = 10
# Génération du sinogramme corrompu en gains / en offsets / les deux
sinogram = gain.reshape(-1, 1) * sinogram + offset.reshape(-1, 1)

plt.imshow(sinogram.T)
plt.show()

# Reconstruction
out = iradon(sinogram, theta=theta, circle=True)
f,ax = plt.subplots(1,2,figsize=(20,10))
ax[0].imshow(img,**ctDisplay)
ax[1].imshow(out,**ctDisplay)
plt.tight_layout()

png

Partie 3 - Interactions avec la matière : rayonnement diffusé

Le rayonnement diffusé est inhérent à la physique des rayons X. Il résulte d’interactions avec la matière (avec le patient, notamment). De deux choses l’une : soit on bloque le rayonnement diffusé avant qu’il n’atteigne le détecteur ; soit on ne le bloque pas, et si on ne corrige pas la mesure par une estimation du diffusé, la qualité image peut s’en trouver réduite.

Questions

Si on calcule toujours $p=\log(I_0)-\log(I)$, mais que cette fois-ci $I$ n’est plus égal au primaire $P=I_0 e^{-p}$, mais au primaire plus le diffusé (autrement dit: $I=P+S$), quelle erreur fait-on sur $p$ ? Les lignes intégrales sont-elles sous-estimées ? sur-estimées ?
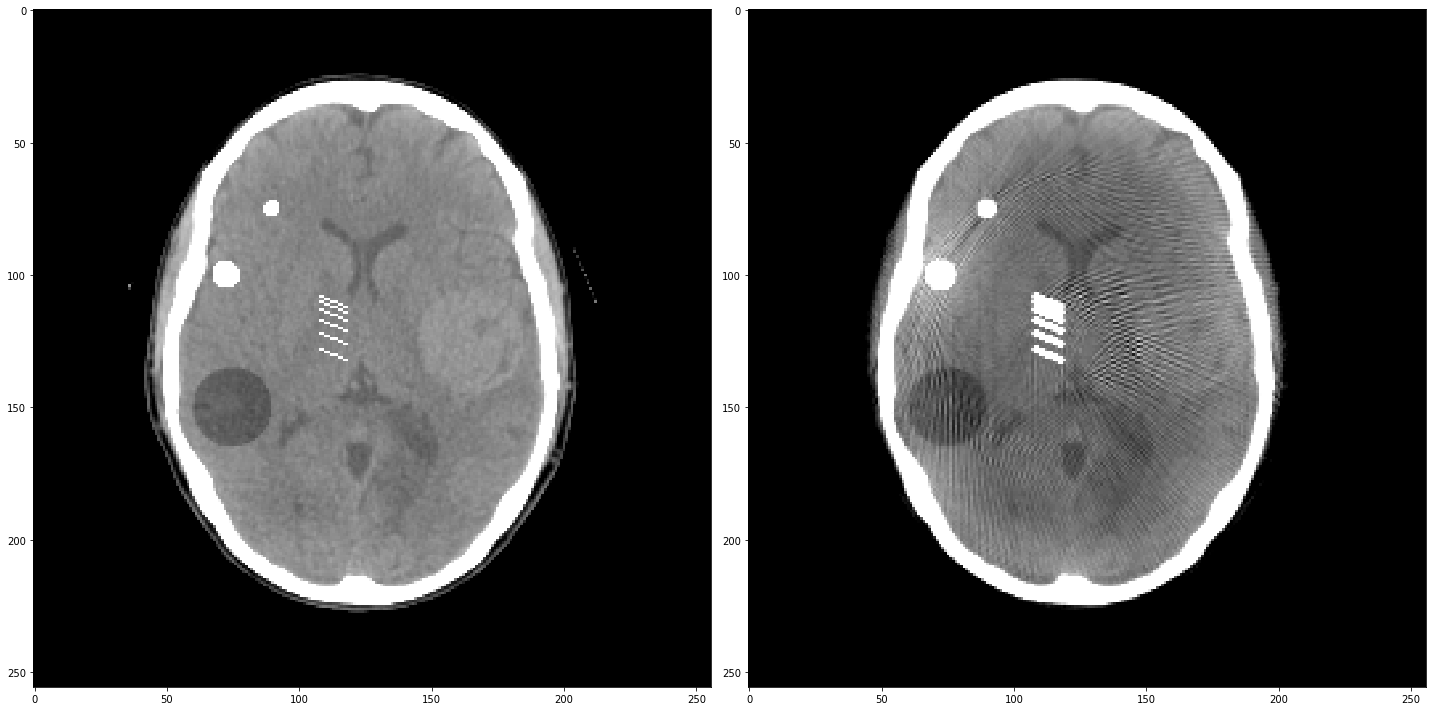
On se propose de simuler un modèle très simple de diffusé ; on suppose que le diffusé ressemble à une versions floutée du rayonnement primaire (celui qui vient directement de la source). Utilisez la fonction gaussian() de skimage pour générer une version lissée du rayonnement primaire (on se fiche de I0 ici, qu’on supposera égal à 1). Prenez sigma=10 comme écart-type du lissage. Ajouter 10% de cette image au primaire, et récupérez le sinogramme associé. Reconstruisez l’image : qu’observez-vous ? Et avec 20%, 30% ?
Calculez le “scatter-to-primary ratio” (ou SPR), égal à $S/P$ ; quelles sont les valeurs de ce ratio ?
$\hat P = P - log(1 + SPR)$

  
from skimage.filters import gaussian

  
# Question 2
sinogram = sinogram0.copy()

# Génération du diffusé
sigma = 10
qty = 0.1

primary = np.exp(-sinogram)
scatter = qty * gaussian(primary, sigma=sigma)

# Génération du sinogramme corrompu en diffusé
sinogram = -np.log(primary + scatter)

# Reconstruction
out = iradon(sinogram, theta=theta, circle=True)
f,ax = plt.subplots(1,2,figsize=(20,10))
ax[0].imshow(img,**ctDisplay)
ax[1].imshow(out,**ctDisplay)
plt.tight_layout()

# Question 3
# SPR
SPR = scatter / primary

plt.figure()
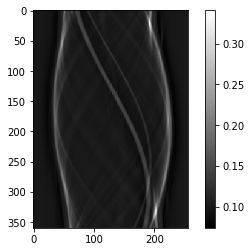
plt.imshow(SPR.T)
plt.colorbar()

<matplotlib.colorbar.Colorbar at 0x7fce4e72f880>

png

La question du diffusé en particulier – et des artefacts en général – est loin d’être anodine ; non seulement la qualité image s’en trouve dégradée, mais pire encore, les applications utilisées en aval (segmentation, recalage, quantification) peuvent voir leurs performances baisser à cause d’une image de mauvaise qualité.

Questions

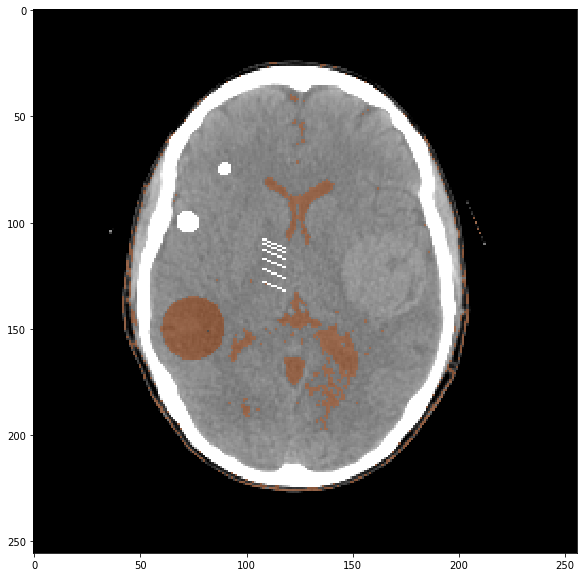
Regardez l’histogramme de l’image CT “propre” ; jouez avec des seuils min et max pour isoler l’hypodensité circulaire dans la tête du patient : y arrivez-vous ? Avez-vous des idées pour nettoyer votre segmentation des pixels segmentés n’appartenant pas à l’hypodensité ?

  
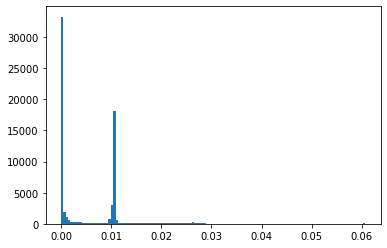
# Question 4
mask = np.zeros(img.shape)
_=plt.hist(img.flatten(),bins=128)
mask[img<0.0104] = 1
mask[img<0.0101] = np.nan
mask[mask==0] = np.nan
plt.figure(figsize=(10,10))
plt.imshow(img,**ctDisplay)
plt.imshow(mask,cmap='hot',alpha=0.3,vmin=0,vmax=2)

<matplotlib.image.AxesImage at 0x7fce4e5dddc0>

png

Questions

Refaites l’exercice, mais sur l’image reconstruite en présence du diffusé à 30%. Comment est l’histogramme des valeurs comparé au précédent cas ? Est-il aussi simple de segmenter l’hypodensité ?

  
# Question 5
mask = np.zeros(img.shape)
_=plt.hist(out.flatten(),bins=128)
mask[out<0.0104] = 1
mask[out<0.005] = np.nan
mask[mask==0] = np.nan
plt.figure(figsize=(10,10))
plt.imshow(out,**ctDisplay)
plt.imshow(mask,cmap='jet',alpha=0.3)

IMED2: TP3

Reconstruction tomographique (2/3)

Partie 1 - Durcissement de faisceau

Questions

Questions

Questions

Questions

Partie 2 - Non-idéalités du détecteur

Questions

Partie 3 - Interactions avec la matière : rayonnement diffusé

Questions

Questions

Questions

Further Reading

IMED2: Project

IMED2: 3D/3D registration with labeled atlas

IMED2: Introduction